3.2 Parallel Lines¶
We know the medians of a triangle are concurrent at a point called the centroid, but proving it requires a result about sets of equally-spaced parallel lines.
- Median
A line passing through a vertex and the midpoint of the opposite side.
A Theorem for the Toolbox
The Transversal Congruence theorem is used only once, but we need it to prove that the medians of a triangle are conurrent.
Transversal Congruence Lemma. If a transversal intersects three parallel lines in such a way as to make congruent segments between the paralllels, then every transversal interesecting these parallel lines will do likewise.
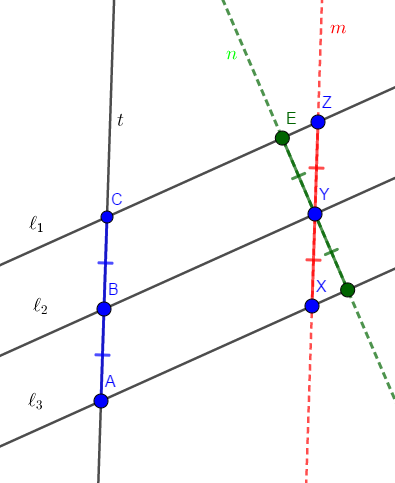
Fig. 9 A sketch of the proof the Transversal Segment Congruence Lemma.¶
Theorems¶
Transversal Congruence Theorem. 1 If a transversal intersects \(n\) parallel lines (\(n>2\)) in such a way as to make congruent segments between the parallels, then every transversal interesecting these parallel lines will do likewise.
Median Concurrence Theorem. The three medians of a triangle are concurent. The concurrency point, called the centroid, is two-thirds of the distant from any vertex to the midpoint of the opposite side.
Hint
Use the Transversal Segment Congruence Theorem to prove the Median Concurrence Theorem.
Two lines parallel to another line are parallel to each other.
If a line intersects one of two parallel llines, then it interesects the other.
- 1
This theorem name is non-standard, invented and used in this document only.
