Contents

The Gnomon

Greek mathematicians were fascinated with the idea of similar figures and patterns. Heron of Alexandria offered the following definition of gnomons.

Gnomon

That which, when added to anything, either number or figure, makes the whole similar to that to which it is added.

Triangular numbers

The Pythagoreans had worked out most of the details regarding triangular numbers and square numbers. They were interested in the shape of certain numbers. The triangular numbers are shown below.

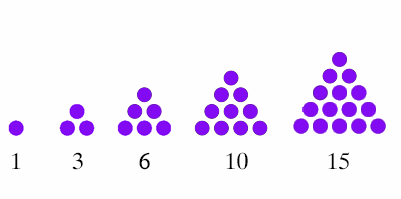
Paralllel lines in hyperbolic geometry

The 3rd and 4th triangular numbers are 6 and 10. Their difference 4 is the gnomon, and we can make a sequence with them. For the triangular numbers, the gnomons are the natural numbers

\[1,2,3,4,\cdots\]

and the partial sums of the gnomons from 1 to 7, for example, will produce the 7th triangular number.

There are square numbers, pentagonal numbers. In fact, there are polygonal numbers of all degrees, and the Pythagoreans investigated many of the low-degree polynomias. They developed relationships between them including the sum of the first \(n\) natural numbers

\[1+2+3+\cdots + n = \frac{1}{2}n(n+1)\]

which is often referred to today as the Gaussian formula. The Pythagoreans probably worked out many of the relationships commonly known today about these relationships.

  1. Any oblong number is the sum of two equal triangular numbers.

  2. Theorem of Theon. Any square number is the sum of two triangular numbers.

  3. Eight times any triangular number plus 1 is a square number.

Project ideas include studying one type of polygonal numbers exclusively, or studying relationships among two or more types. The series created by the gnomons are a common thread in the theorems the Greek developed, and any project should include some of the “dots” drawings the Greeks used to prove them.

Geometric and Harmonic Means

The Greeks often thought of a mean as completing a pattern, for example the geometric mean where

\[\frac{a}{x} = \frac{x}{b}\]

is solved by finding a value \(x\) that makes the relationship true. Once found, \(x\) is between \(a\) and \(b\) and, if \(a<b\), then \(\dots,a,r,b,\dots\) are consecutive terms of a geometric sequence. The above equation has the solution \(x = \sqrt{ab}\) so that

\[\frac{a}{\sqrt{ab}} = \frac{\sqrt{ab}}{b}\]

A simple example shows the relationship:

\[\frac{2}{\sqrt{2(8)}} = \frac{\sqrt{2(8)}}{8} \implies \frac{2}{4} = \frac{4}{8}\]

The common ratio of the geometric sequence can be found by

\[ar = \sqrt{ab} \implies r = \frac{\sqrt{ab}}{a} = \sqrt{\frac{b}{a}}\]

The geometric mean has interesting and wide ranging applications including analyzing investment portfolios. The Greeks developed more than a dozen “means,” several of which are still in use today, including the harmonic mean.

Project Ideas

  1. Triangular numbers

  2. Rectangular numbers

  3. Pentagonal numbers

  4. Polygonal numbers such as hexagonal, octagonal, etc.

  5. Relationships between types of polygonal numbers

  6. Geometric mean

  7. Harmonic mean

  8. The Greek idea of means

  9. Gnomons and related ideas (any of these could be a project, and other project ideas related to gnomons exist)

    1. Spirals

    2. Golden Ratio

    3. Golden Rectangle

Geometry Projects Quadrature