3.5 Circles¶

Chord: A line segment joining two of the points of the circle.
Secant: A line which contains a chord.
Tangent: A line which contains exactly one point of a circle.
Radius: The distance from the center to any point on the circle. Also used to refer to a segment which joins
Diameter: The length of a chord which passes through the center of the circle.

Tip

Radii and diameters are defined primarily as distances. It’s also helpful to refer to line segments that have the corresponding lengths as radii or diameters.

Central Angle: Any angle whose vertex is the center of a circle.
Arc: The set of points on a circle that lie between two points on the circle, including the points themselves. The degree measure of an arc is the measure of the central angle corresponding to the arc. Each two points on a circle create two arcs, a minor arc and a major arc, with the degree measure of the major arc greater than (or equal to) that of the minor arc.
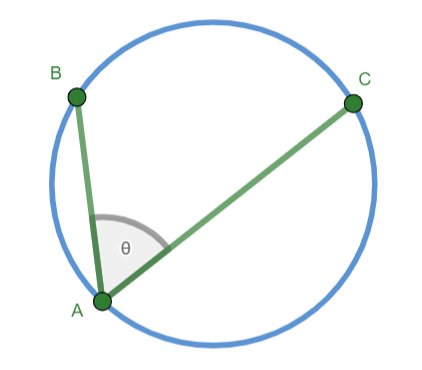
Inscribed Angle: The angle formed when two secant lines intersect on the circle.

Intercepted Arc: The part of the circle that lies between two lines that intersect it.

Theorems¶

In the Euclidean plane, three distinct points uniquely determine a circle. (Requires both an existance proof and a uniqueness proof.)
If \(\overline{AB}\) is a diameter and \(\overline{CD}\) is any other chord of the same circle (which is not a diameter), then \(AB>CD\).
If a diameter of a circle is perpendicular to a chord of the circle, then the diameter bisects the chord.
The perpendicular bisector of a chord of a circle contains a diameter of the circle.
If a line is tangent to a circle, it is perpendicular to the line joining the point of tangency to the center of the circle.
Arc Addition. If \(\overset{\Huge\frown}{ABC}\) and \(\overset{\Huge\frown}{CDE}\) are arcs sharing only the same endpoint \(C\), then \(m\overset{\Huge\frown}{ABC}+m\overset{\Huge\frown}{CDE}=m\overset{\Huge\frown}{ACE}\).
Inscribed Angle Theorem. The measure of an angle inscribed in an arc is one-half the measure of its intercepted arc.

Note

The measure of an arc is equal to the measure of the central angle corresponding to the arc.
Two-Chord Angle Theorem. If two chords interesect in the interior of a circle to determine an angle, the measure of that angle is the average of the measures of the arcs intercepted by the angle and its vertical angles.

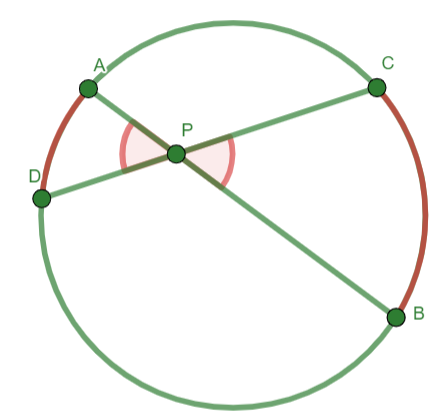
Fig. 14 Two-Chord Angle Theorem¶
Two-Secant Angle Theorem. If two secants interesect in the exterior of a circle to determine an angle, the measure of the angle at the point of intersection is one-half the positive difference of the two intercepted arcs.

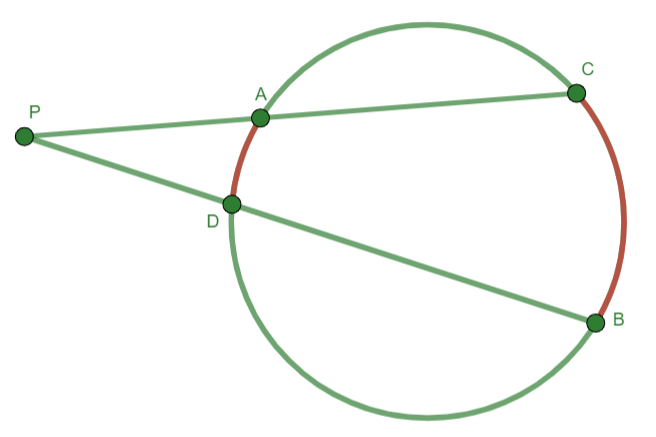
Fig. 15 Two-Secant Angle Theorem¶
Tangent-Chord Angle Theorem. If \(\overleftrightarrow{AB}\) is tangent to a circle at \(A\), and if \(\overline{AC}\) is a chord of the circle with \(m\overset{\Huge\frown}{APC}=x^{\circ}\), then \(m\angle BAC=\frac{x^{\circ}}{2}\).

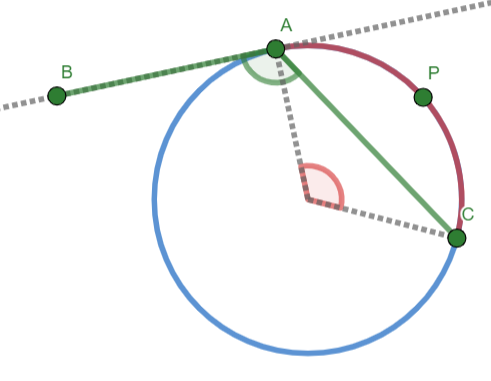
Fig. 16 Tangent-Chord Angle Theorem¶
Two-Tangent Angle Theorem. The measure of an angle formed by two tangents drawn to a circle is one-half the positive difference of the measures of the intercepted arcs.

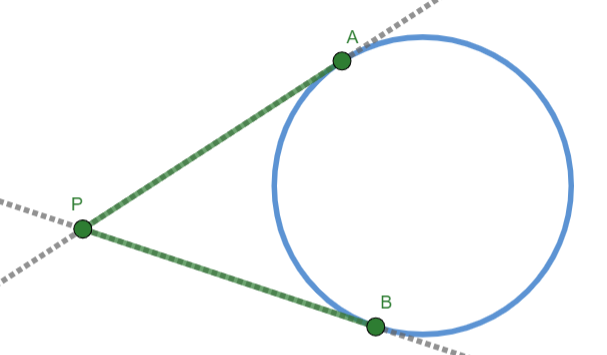
Fig. 17 Two-Tangent Angle Theorem¶
Corollary to the Two-Tangent Angle Theorem. Tangent segments drawn to a circle from the same (exterior) point are congruent.
Chord Segment Product Theorem. If two chords of a circle intersect, the products of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other.

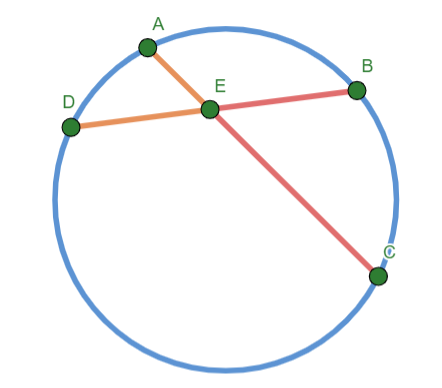
Fig. 18 Two-Tangent Angle Theorem¶
Secant Segment Product Theorem. If two secant lines are drawn to a circle from the same exterior point, then the product of the length of the secant segment and the lenth of its exterior portion is the same for both secants.

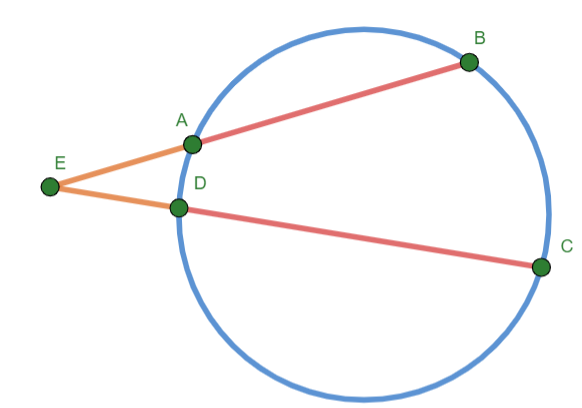
Fig. 19 Two-Tangent Angle Theorem¶

Geometry

3.5 Circles¶

Theorems¶