A.2 Proofs in Analytic Geometry¶

Use analytic geometric techniques to prove the following well-known Euclidean geometry theorems. Make sure to pick the origin and axes so that the arbitrary figure is located helpfully with respect to the axes and has a useful orientation. Then use Euclidean theorems and equations of lines to prove the needed result.

Theorems¶

Two lines with slopes \(m_1\) and \(m_2\) are perpendicular provided

\[m_2 = -\frac{1}{m_1}\]

Hint

Most analytic geometry proofs are made much easier if we choose the coordinate system wisely. For the above proof, place the origin at the intersection of the two lines.
Two distinct lines with the same slope are parallel.
A quadrilateral ABCD is a parallelogram if and only if both pairs of opposite sides are congruent.

Hint

Always choose your coordinate system to make life easier. For the above proof, place the line segment \(\overline{AB}\) on the \(x\)-axis such that \(B=(0,0)\) and \(A=(a,0)\). Locate \(C\) and \(D\) in the first quadrant.

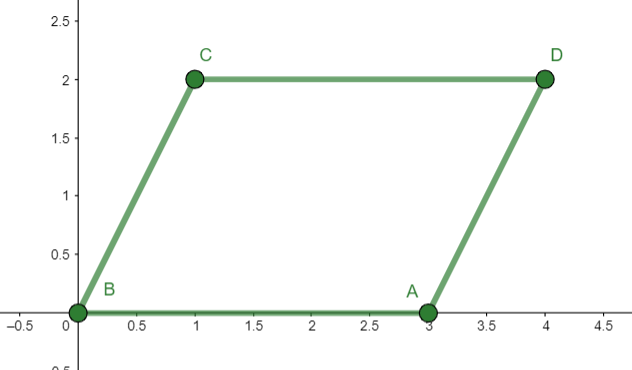
Fig. 20 Placing coordinates for a parallelogram proof in analytic goemetry.¶
The diagonals of a parallelogram bisect each other.

Hint

Use same coordinate setup shown above.
The set of all rectangles with area equal to \(1\) which have a vertex at the origin satisfy the relationship \(y=\frac{1}{x}\).
Given the vectors \(\vec v\) and \(\vec u\) have the same “tail,” the parallelogram