Contents

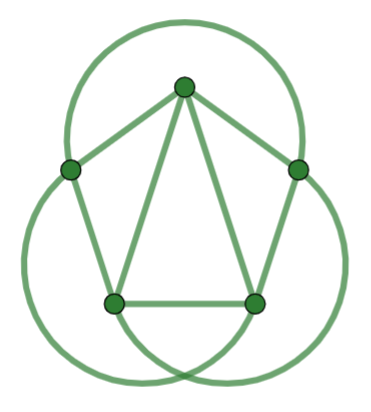
1.3 Five Point Geometry

The Five Point Geometry (5PG) uses the standard undefined and defined terms for finite geometry.

Undefined Terms

Point, Line and On

Defined Terms

Parallel, Intersect and Concurrent

../_images/Fig2_5PG.png

Fig. 2 Model for the Five Point Geometry

Axioms for the 5PG

  1. There exist exactly five points.

  2. Any two distinct points have exactly one line on both of them.

  3. Each line is on exactly two points.

Tip

The only difference between the axioms for the 4PG and 5PG is the word “four” changing to “five” in the first axiom.

5PG Theorems

  1. How many distinct lines are in the Five Point Geometry? Prove your conjecture.

  2. Prove or disprove: There exists a set of two lines in the Five Point Geometry that contain all of the points in the geometry. If you disprove this statement, change the word in bold so that the theorem is true, and prove the new theorem.

We will return to Five Point Geometry later when we discuss affine geometries. The next two finite geometries are iconic: Fano’s Geometry and Young’s Geometry.

1.2 Four Point Geometry 1.4 Fano’s Geometry