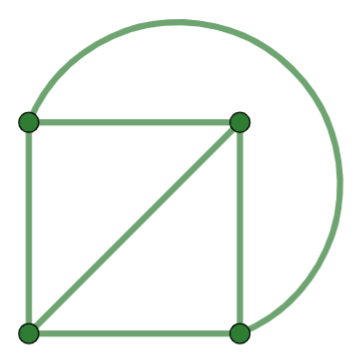
1.2 Four Point Geometry¶
The Five Point Geometry (5PG) uses the standard undefined and defined terms for finite geometry.
Undefined Terms
Point, Line and On
Defined Terms
Parallel, Intersect and Concurrent
Fig. 1 Model for the Four Point Geometry¶
The axioms below together with the standard undefined terms for finite geometry describe the Four Point Geometry (4PG).
Axioms for the 4PG
There exist exactly four points.
Any two distinct points have exactly one line on both of them.
Each line is on exactly two points.
We would normally say two lines intersect if they contain the same point. However, we have not defined what contain means. We use the undefined term “on” to refer both to a line being on some points and to points being on a line.
4PG Theorems¶
In the Four Point Geometry, if two lines intersect, they have exactly one point in common.
The Four Point Geometry has exactly six lines.
In the Four Point Geometry, each point has exactly three lines on it.
In the Four Point Geometry, each line has at least one line that is parallel to it.
Prove that there exists a set of two lines in the Four Point Geometry that contain all of the points in the geometry.
The Four Point Geometry can be extended to five, six or more points by simply changing the first axiom. We will explore the Five Point Geometry in the next section, but some of the properties will be different.