Contents

1.5 Young’s Geometry

Warning

Changing a single axiom can generate a very different geometry.

Young’s Geometry is identical to Fano’s Geometry except for Axiom 5. Young’s geometry appears to be named for American mathematician John Wesley Young who, along with Oswald Veblen, published a seminal treatise on projective geometry just before World War I. There is confusion at times between the 20th century American mathematician and several British matheticians with the same surname. Young spent the majority of his career at Dartmouth University and was president of the American Mathematical Society from 1929 - 1930.

We again use the standard undefined and defined terms.

Undefined Terms

Point, Line and On

Defined Terms

Parallel, Intersect and Concurrent

Axioms for Young’s Geometry

  1. There exists at least one line.

  2. There are exactly three points on each line.

  3. Not all points are on the same line.

  4. There is exactly one line on any two distinct points.

  5. For each line \(l\) and each point \(P\) not on \(l\), there exists exactly one line on \(P\) that does not contain any points on \(l\).

Even though the only minor difference in the geometries is Axiom 5, they have very different properties. The Model for Young’s Geometry is shown below. Note that each line contains three points, so some of the lines (shown in red and orange) curve around the outside of the square. There are no intersections except where points appear.

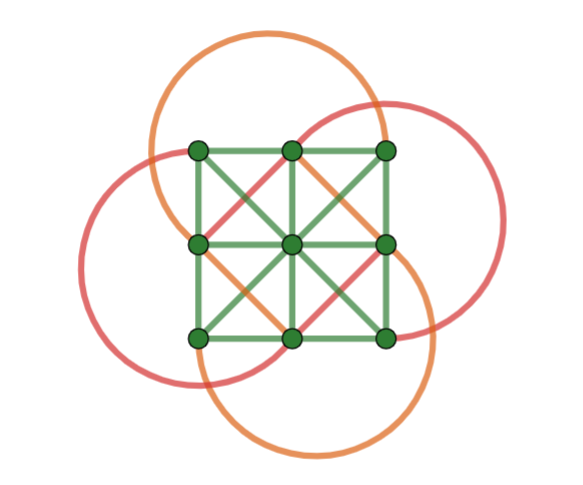
../_images/Fig4_Young.png

Fig. 4 Model for Young’s Geometry

Theorems for Young’s Geometry

  1. In Young’s Geometry, there exist at least four points.

  2. Laurel’s Lemma. 1 In Young’s Geometry, for each point \(P\) there exists least one line \(l\) that does not contain it.

  3. In Young’s Geometry, every point is on at least four lines.

  4. In Young’s Geometry, every point is on at most four lines

    Note

    Theorems 3 and 4 together show how to prove every point is on exactly four lines.

  5. In Young’s Geometry, let \(l \parallel m\). If line \(n\) intersects \(l\), it intersects \(m\) also.

  6. In Young’s Geometry, two lines parallel to a third line are parallel to each other.

  7. Young’s Geometry contains exactly nine points.

    Hint

    Prove first that at least 9 points exist. Next, that no more than 9 points exist.

  8. In Young’s Geometry, every line has exactly two distinct lines that are parallel to it.

  9. Young’s Geometry contains exactly twelve lines.

1

Helpful theorem proposed and proved by a former student at UNG.

1.4 Fano’s Geometry 1.6 Searching for a Parallel Posutlate