Contents

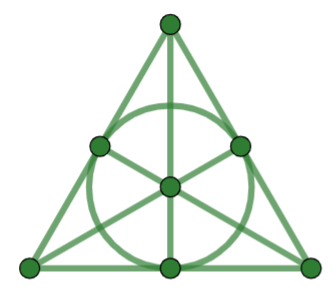
1.4 Fano’s Geometry

Image: Gino Fano Gino Fano (1871 - 1952)

Gino Fano was the founder of finite geometry. He created and explored the projective geometry of order 2 which bears his name. The Fano Plane is the smallest possible finite projective geometry, the one with the fewest points and lines.

We use the standard undefined terms and defined terms for finite geometry, just as with the 4PG and 5PG.

Undefined Terms

Point, Line and On

Defined Terms

Parallel, Intersect and Concurrent

Axioms for Fano’s Geometry

  1. There exists at least one line.

  2. There are exactly three points on each line.

  3. Not all points are on the same line.

  4. There is exactly one line on any two distinct points.

  5. There is at least one point on any two distinct lines.

Theorems

../_images/Fig3_Fano.png

Fig. 3 Model for Fano’s Geometry

  1. In Fano’s Geometry, there exist at least four points.

  2. Lindsey’s Lemma. 1 For every point \(P\) in Fano’s Geometry, there exists a line that does not contain it.

    • Lemma 1. Fano’s Geometry contains at least seven points.

    • Lemma 2. Fano’s Geometry contains no more than seven points.

    Note

    Lemmas 1 and 2 together prove Theorem 3, that Fano’s Geometry contains exactly seven points.

  3. Fano’s Geometry contains exactly seven points.

  4. Fano’s Geometry contains exactly seven lines.

    Hint

    Use two different proofs, like the lemma approach above.

  5. In Fano’s Geometry, each line is on exactly three points.

  6. In Fano’s Geometry, the set of all lines on a single point contains all the points in the geometry.

  7. In Fano’s Geometry, for every pair of points, there exist exactly two lines containing neither point.

  8. In Fano’s Geometry, each point is on exactly three lines.

1

Helpful theorem proposed and proved by a former student at UNG.

1.3 Five Point Geometry 1.5 Young’s Geometry