Conditional Probability

It is often far easier to count the outcomes in the complement of event \(A\), e.g. the probability that event A does not occur. We denote the set complement as \(\overline A\). The formula is:

The probability of \(A\) occurring given that event \(B\) has \emph{already occurred} is the \textbf{conditional probability} of \(A\) given \(B\):

\[P(A|B)=\frac{P(A\cap B)}{P(B)}\]

In many conditional probability situations, we can solve for the required probability by restricting the probability space.

Example

A card is drawn at random from a standard deck of playing cards.What is the probability of drawing a heart (\(H\)) given that a red card (\(R\)) is drawn?

Solution. Half of the red cards are hearts.

\[P(H|R)=\frac{1}{2}\]

We often can simply work with a new probability space - the red cards - rather than employing the formula. Yet, the formula works, too.

\[P(R) = \frac{1}{2}\]

\[\hspace{1cm}P(H\cap R) = \frac{1}{4}\hspace{5mm}\implies\]

\[P(H | R) =\frac{P(H\cap R)}{P(R)}= \frac{\frac{1}{4}}{\frac{1}{2}}=\frac{1}{4}\cdot \frac{2}{1}=\frac{1}{2}\]

We use conditional probability to define independent probability events. The idea? If events \(A\) and \(B\) are independent, then \(B\) happening - or not - should not affect the likelihood of \(A\) happening.

1. Defintion. Let the event sets \(A\) and \(B\) be subsets of a probability space \(S\). Events \(A\) and \(B\) are said to be independent provided:

\[P(A)=P(A|B)\]

This implies that \(P(B)=P(B|A)\). To see that \(P(A)=P(A|B)\iff P(B)=P(B|A)\):

\[P(A|B) = P(A)\hspace{5mm}\iff\]

\[P(A)P(B) = P(A\cap B)\hspace{5mm}\iff\]

\[P(B|A) = P(B)\]

Example

Is drawing a face card (\(F\)) is independent of drawing a red card (\(R\))?

Solution. There are 12 face cards. Half the deck and half the face cards are red cards.

\[P(F) = \frac{12}{52}=\frac{3}{13}\]

\[P(R) = \frac{1}{2}\]

\[P(F\cap R) = \frac{6}{52}=\frac{3}{26}\hspace{5mm}\implies\]

\[P(F|R) = \frac{P(F\cap R)}{P(R)} = \frac{\frac{3}{26}}{\frac{1}{2}}=\frac{3}{26}\cdot\frac{2}{1}=\frac{6}{26}=\frac{3}{13}\]

Since \(P(F|R)=\frac{3}{13}=P(F)\), the events are independent.

Example

At Riverside High School, the probability that a student takes Computer Programming and Spanish is 0.15. The probability that a student takes Computer Programming is 0.4. What is the probability that a student takes Spanish (\(S\)) given that the student is taking Computer Programming (\(C\))?

Solution. Note that \(P(S\cap C)= 0.15\) and \(P(C) = 0.4\).

\[P(S|C)=\frac{0.15}{0.4} = \frac{15}{40}=\frac{3}{10}\]

The next example focuses on visualizing the relationship of the event sets when probabilities are independent.

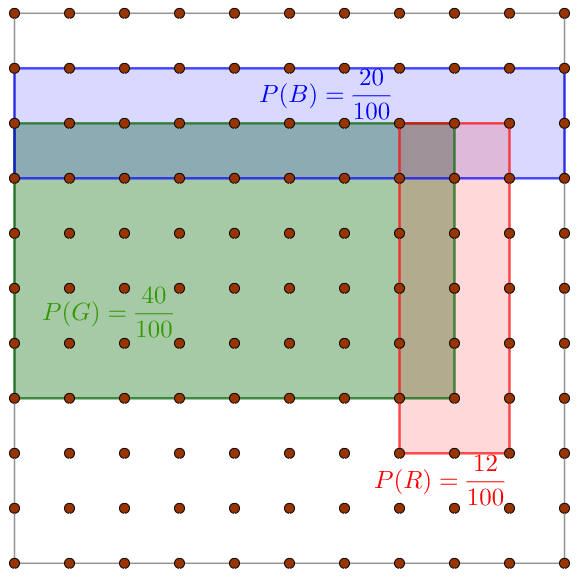
Fig. 9 Conditional Probability Visualization

Example

The events sets \(R,B,G\) are shown above as subsets of a probability space represented by a \(10\times 10\) grid. Determine if any of the event sets are independent given that \(P(G)=\frac{2}{5}\), \(P(B)=\frac{1}{5}\), and \(P(R)=\frac{3}{25}\).

Solution. Visually, notice that \(20\%\) of the green squares are also blue and that \(P(B)=20\%\). It appears that \(B\) and \(G\) are independent. Checking the other relationship visually, note that 8 of the 20 blue squares are also green (\(40\%\)), and that \(P(G)=40\%\).

We can also use the formulas.

\[P(B|G) = \frac{P(B\cap G)}{G}\]

\[= \frac{\frac{8}{100}}{\frac{40}{100}}\]

\[=\frac{8}{40}\]

\[=\frac{1}{5}=P(B)\]

The other two pairs of sets are not independent.

\[P(G|R)=\frac{5}{12}\neq P(G)\hspace{5mm}\text{and}\hspace{5mm}P(B|R)=\frac{1}{50}\neq P(R)\]