Counting Patterns#
Most people learn, even if they don’t remember, about combination and permutations. There are more than these two counting patterns that we use regularly in probability problem-solving, and we will discuss the most important.
Basic Counting Patterns#
We have two kinds of draws \emph{without replacement}, combinations and permutations, but what about draws with replacement? Their structure means we count the possible arrangements in the same way we find the cardinality of sets that are Cartesian products: we multiply.
A Cartesian product of two sets \(A\) and \(B\) is the set of all ordered pairs \((a,b)\) where the first item is drawn from set \(A\) and the second is drawn from set \(B\):
The \(xy\)-coordinate plane is familiar to most. Cartesian coordinates are used to identify points in the plane. Order matters, because the point \((1,6)\) is different from \((6,1)\). The coordinate plane is the Cartesian product \(\mathbb R\times\mathbb R\). While the set of real numbers is infinite, we often use finite sets for Cartesian products in probability settings.
Example 7
A 6-sided die is rolled and a coin is flipped. List the elements of the Cartesian product and determine its cardinality.
Solution. Let the set \(D\) represent the possible outcomes to rolling the fair, 6-sided die, and let the set \(C\) represent the possible outcomes when flipping a fair coin:
We can arrange the ordered pairs \((d,c)\) to highlight the similarity to Cartesian coordinates:
Since \(|D|=6\) and \(|C|=2\), the total number of outcomes in the Cartesian product \(D\times C\) is 12 because:
Example 8
How many Georgia license plates are possible given the standard pattern is 3 letters followed by 4 numbers?
Solution. If \(L\) represents the set of 26 letters in our alphabet and \(D\) represents the base 10 digits, then possible license plates form a Cartesian product: \(L\times L\times L\times D\times D\times D\times D\). The number of possible license plates is given by
The number of outcomes in a Cartesian product is the product of the cardinalities of each set in the Cartesian product.
Special Counting Patterns#
The primary tools for counting in a probability context have already been discussed: permutations, combinations, Cartesian products and partitioning the probability space into disjoint subsets. Some additional tools are helpful but seen much less often.
Handshake Problem#
Two classic mathematics idea merge in the handshake problem.
Example 8
Ten people attend a party. During the event, each party goer shakes hands with every other person. How many handshakes happened?
Solution. Once we find the pattern, the solution is straightforward. Consider attendees at the party: Al, Bea, Cal, Di,…

Fig. 1 height: 200px#
Ten people at party, Al shakes hands with 9 others, Bea shakes hands with 8 others, and so on.
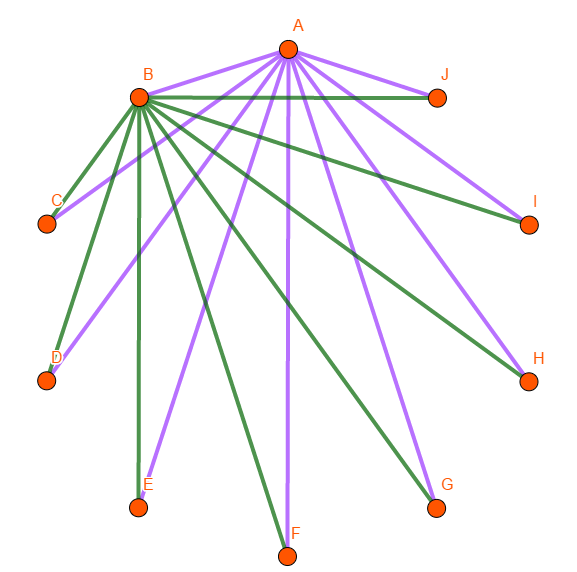
Fig. 2 height: 250px#
If Al shakes hands with everyone, there are 9 handshakes. Then, say Bea shakes hands with everyone she has not shaken hands with, yet. That will create 8 more handshakes. Then Cal, who has shaken hands twice, once with Al and once with Bea, will complete 7 more handshakes, and so on. Thus, the total number of handshakes for all 10 people is:
The sum of all positive integers from \(1\) to \(n\) is the classic pattern attributed to Gauss. The story goes like this: little Freddie is precocious, and his tutor can’t write math problems quickly enough. By the time he gets one written down, Freddie has solved it, and the tutor has no time for any other subject or any other child. In exasperation, the tutor challenges the adolescent math whiz: “Add up all the numbers between one and one hundred.” Surprisingly, Freddie answer almost immediately: “Five thousand and fifty.” He saw the pattern shown below.
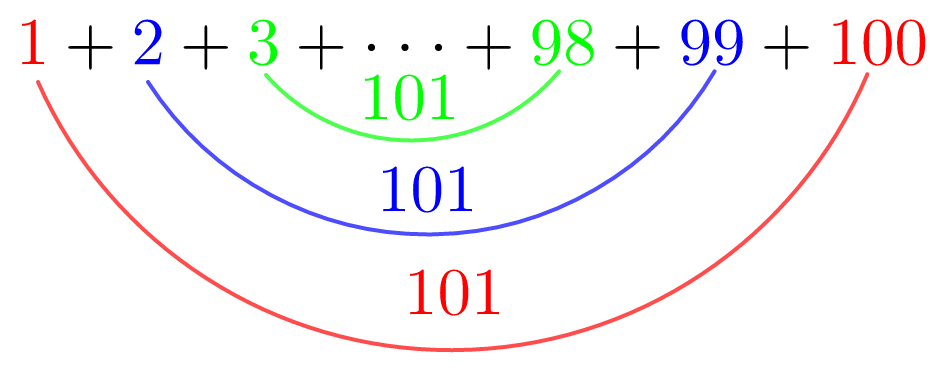
Fig. 3 The Gauss pattern for summing integers from 1 to 100#
There are 50 pairs of integers that sum to 101, so he multiplied quickly to find the sum: \(50\times 101=5050\).
While formulas exist (you can google “Gauss’s formula”) I encourage you to learn Gauss’s idea instead of memorizing some formula, or at least to derive the formula for yourself (it’s not hard). The formula works not only for this exact situation. The idea works for the sum of any finite number of terms in any arithmetic sequence.
The birthday problem counting pattern is iconic, as is Gauss’s approach, and any student of mathematics taking a course that includes principles of counting should learn about them.
Permutations on a Ring#
Example 9
A mom of five gets a charm bracelet with each child’s name on a charm. How many permutations of the charms are possible?
Solution. If her children were named Dee, Eve, Fay, Gil and Hal, it’s tempting to consider it like permutation five items into five slots:
where the letters would line up:
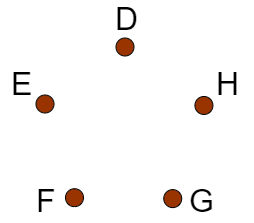
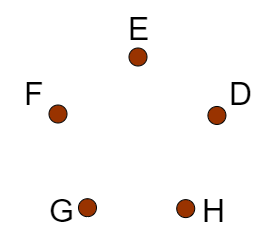
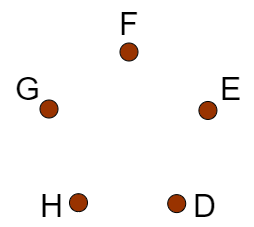
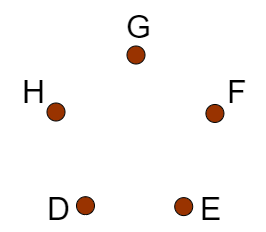
That approach turns out to be incorrect. When spaced equally on a circle, there are five identical patterns that correspond to
Those patterns are shown below:
The same thing is true for every unique permutation of five items on a ring or on a circle. We have the permutation plus four identical copies. To correct for this, we have to divide by 5. Let \(C_5\) be the set of all possible permutations of five objects on a circle.
Most students remember that, in general, the number of permutations of \(n\) objects on a circle is given by:
When studying permutations in Abstract Algebra (UNG course MATH 4600), we learn cycle notation for writing down the individual permutations in a permutation group. An \(n\)-cycle represents \(n\) different versions of the exact same permutation, so we use a quick fix for notation: always list the smallest digit in the cycle first. That way, we have a unique representation for permutations, similar to the unique lowest terms form of a fraction.