Worked Examples#

With discrete probability functions, we have two main tasks:

  1. Solve for and find a closed form equation for the probability density function (pdf).

  2. Use pdf in probability problem-solving.

We will need our combinations and permutations formulae:

combin <- function(n, k) {
    return(factorial(n) / ( factorial(k)*factorial(n-k) )) }
perm <- function(n, k) {
    return(combin(n,k) * factorial(k))}

Let’s do some mixed practice.

Example 1: Pocket Pairs in Texas Holdem#

In Texas Holdem, players are dealt 2 cards face down to begin. When those 2 cards have the same value as in JJ, the player is said to have a pocket pair. What is the probability that Hero sitting in at a new poker table sees his first pocket pair on the fifth hand dealt to him?

Solution#

Probability of Single Event#

We first need to determine the probability of success. What is the probability of being dealt a pocket pair on any one hand? Let \(\textbf{pp}\) be the event of drawing a pocket pair, and we have the following:

\[P(\textbf{pp}) = \frac{\binom{13}{1}\binom{4}{2}}{\binom{52}{2}}=\frac{1}{17}\]
combin(13,1) * combin(4,2) / combin(52,2)
0.0588235294117632

We show some simplifications in the screen shot below after noting that:

  • \(\binom{13}{1}=13\)

  • \(\binom{4}{2}=6\)

  • \(\binom{52}{2}=1326\)

The screenshot below indicates how, with a standard TI graphing calculator, we can reduce a rather complicated fraction to lowest terms.

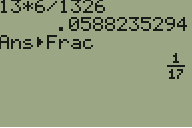
_images/Ti7.png

Fig. 12 Simplifying the Fraction#

Probability Density Function#

The probability of drawing a pocket pair on the 1st, 2nd, 3rd, or 4th hand is show below. Since \(\frac{16}{17}\) is probability of not succeeding, a string of fractions will describe what’s happening:

  1. Probability of \(\textbf{pp}\) on 1st hand: \(\frac{1}{17}\)

  2. Probability of \(\textbf{pp}\) on 2nd hand: \(\left(\frac{16}{17}\right)\left(\frac{1}{17}\right)\)

  3. Probability of \(\textbf{pp}\) on 3rd hand: \(\left(\frac{16}{17}\right)\left(\frac{16}{17}\right)\left(\frac{1}{17}\right)\)

  4. Probability of \(\textbf{pp}\) on 4th hand: \(\left(\frac{16}{17}\right)\left(\frac{16}{17}\right)\left(\frac{16}{17}\right)\left(\frac{1}{17}\right)\)

Identifying the pattern of \(n-1\) failures followed by a success, we see that probability of \(\textbf{pp}\) on nth hand is given by:

\[P(\text{nth hand success}) = \left(\frac{16}{17}\right)^{n-1}\left(\frac{1}{17}\right) \hspace{3mm}\text{ where }n\in \{1,2,3,\cdots\}\]

This is a geometric probability distribution.

Solutions#

  1. What is the probability that Hero sees his first pocket pair on the fifth hand dealt?

\[P(\text{success: }n=5) = \left(\frac{16}{17}\right)^{4}\left(\frac{1}{17}\right)=\frac{16^4}{17^5}\approx 0.046157\]
16^4 / 17^5
0.0461567608569032

  1. What is the probability that Hero sees his first pocket pair on the tenth hand dealt?

\[P(\text{success: }n=10) = \left(\frac{16}{17}\right)^{9}\left(\frac{1}{17}\right)=\frac{16^9}{17^{10}}\approx 0.034087\]
16^9 / 17^10
0.0340871451648216

Example 2: Oil Wells#

An energy company has leased an undeveloped oil field where they estimate a 35% chance of success for drilled wells striking oil. They have enough funds to drill 7 oil wells, but to turn a profit they need at least 3 of those wells to strike oil. What is the probability that their 3rd success occurs on their 7th drilled well?

Patterns#

Consider if the company had its 3rd success on its 5th drilled well. Note that the last well drilled must be success, so some of the possible patterns are as follows:

  • S S F F S

  • S F S F S

  • F S S F S

  • F S F S S

  • S F F S S

So, in the first 4 slots, we must choose 2 slots to be successes while the others are failures. The last slot is fixed as a success. Let \(X\) represent the set of numbers for the last wells drilled. So, \(X = \{3,4,5,6,7\}\) Hence, the probability for the fifth-well success would be:

\[P(x=5) = \binom{4}{2}(0.35)^2(0.65)^2(0.35)\]

In the above probability calculation, the last factor of \((0.35)\) is isolated to show that the last well drilled is a succes. We can combine this as follows: $\(P(x=5) = \binom{4}{2}(0.35)^3(0.65)^2 \)$

Analyzing the succees-fail patterns for \(x=6\), we find that:

\[P(x=6) = \binom{5}{2}(0.35)^3(0.65)^3\]

Thus, the probability that \(x\in X\), the last well drilled, achieves overall success is as follows:

\[P(X=x) = \binom{x-1}{2}(0.35)^3(0.65)^{x-3}\]

This is the negative binomial distribution. To see that this is the correct expression for the closed form version of the this pdf:

  1. When \(x=3\), we have three successess immediately. This means we will have \(\binom{2}{2}=1\) to arrange the first 2 successes into the first 2 slots. There are 3 successes in all cases, so we have \((0.35)^3\). The exponent for the last factor is \(0\) because no failures occured.

  2. When \(x=4\), we use the reasoning explained above.

  3. The pattern holds if we understand what each factor in the probability indicates.

Solutions#

  1. Find the probability the oil company hits 4 successful wells on the 6th well dug. For \(k=4\) successes, we have:

\[P(X = 6, k=4) = \binom{5}{3}(0.35)^4(0.65)^2\]
combin(5,3) * 0.35^4 * 0.65^2
0.06340140625

  1. Find the probability the oil company hits 4 successful wells on the 5th well dug.

\[P(X = 5, k=4) = \binom{4}{3}(0.35)^4(0.65)\]
combin(4,3) * 0.35^4 * 0.65
0.03901625

Example 3: Card Game Spades#

Cards from the spade suit are valuable in the card game Spades. When played with 4 players, the entire deck is dealt out so that each player receives 13 cards. What is the probability that a player is dealt 7 or more spades?

The Pattern#

This is very similar to questions we solved using partitions. Let \(X\) be the set outcomes specifying the number of spades in our hand, e.g. \(X=\{1,2,3,\cdots,13\}\). The we have the probability of exacctly 4 spades:

\[P(X = 4) = \frac{\binom{13}{4}\binom{39}{9}}{\binom{52}{13}}\]

We draw 4 cards from within the spades suit partition which has 13 cards, and 9 cards from the remaining 39 cards in the deck.

The pdf#

\[P(X = x) = \frac{\binom{13}{x}\binom{39}{13-x}}{\binom{52}{13}}\]

Solutions#

  1. Find the probability of being dealt a spades hand with 7 spades.

\[P(X = 7) = \frac{\binom{13}{7}\binom{39}{6}}{\binom{52}{13}}\]
p = combin(13,7) * combin(39,6) / combin(52,13)
p
0.00881660081640865

  1. Find the probability of being dealt a spades hand with 6 or more spades.

\[P(6\leq x\leq 13) = \sum_{k=6}^{13}\frac{\binom{13}{k}\binom{39}{13-k}}{\binom{52}{13}}\]

For this summation, we need a FOR loop like we did in the binomial section:

tab <- c()            ## Empty vector to store all the terms 
lo = 6                ## LEAST Number of successes
hi = 13               ## MOST Number of successes
k = 1                 ## Indexing variable for tab vector

for (t in lo:hi){
    tab[k] <- combin(13,t) * combin(39,13-t) / combin(52,13)      # Calculate the term and save in the vector "tab"
    k <- k + 1
}
sum(tab)

tab
0.051644298374758
  1. 0.0415639752773551
  2. 0.00881660081640865
  3. 0.00116690304923056
  4. 9.26113531135363e-05
  5. 4.11606013837939e-06
  6. 9.10185288585123e-08
  7. 7.98408147881687e-10
  8. 1.57476952244909e-12