Expected Value

Professional gamblers often talk about the equity or EV of their playing decisions. Poker pros think of every bet and call as an investment. Professional investors on Wall Street think in the same terms. EV stands for expected value, and positive EV is good. In both gambling and investing in the stock market, there is no guarantee that positive EV will lead to a positive outcome. Yet, on average and over time, playing with positive EV will win money. Negative EV is bad - it’s means the play loses money on average.

Definitions

• The expected value of a simple random variable \(x\in X\) is given by:

\[E(X)=\sum x_iP(x_i)\]

for all \(i\) such that \(x_i\in X\). The expected value is often referred to as the mean of \(X\) and written as

\[\mu_X=E(X)\]

• The variance of a simple random variable \(x\in X\) is given by:

\[V(X) = E\left(X^2\right)-E\left(X\right)^2\]

Note that, since \(\mu_X=E(X)\), we can write variance as follows:

\[V(X) = E\left(X^2\right)-\mu_X^2\]

• The standard deviation is the square root of the variance:

\[\sigma_X^2=V(X)\]

The expected value of a probability experiment is the value that, on average, one would expect to earn if the experiment were repeated many, many times. The variance measures how widely the different outcomes spread apart. We generally prefer standard deviation over the variance because the standard deviation is in the same the units as the original outcomes.

Why do millions of reasonably intelligent people play the lottery which has an expected value of \(\mu_X\approx -\$0.33\) for every dollar invested? Because of the extremely high variance. Yes, most times you lose a little bit of money, but the huge variance means that, if you win, you win really, really big. Slot machines with their \(\mu_X \approx -\$0.05\) per dollar work on the exact same principle, but on a much smaller scale. In fact, most gambling games take advantage of this alluring facet of probability theory: small, negative expected values paired with huge variance so that, if you do win, you have story to tell.

Examples

Expected value and variance calculations are not difficult. Several examples should suffice to see how the calculations work, and calculator tips are given, as well.

Die Roll

What is the expected value, variance and standard deviation of rolling a standard, fair, 6-sided die?

Expected Value

We start with our expected value formula and substitute the correct values for our given scenario. The calculations and simplifications follow:

\[\begin{split}\begin{align}E(X)&=\sum x_iP(x_i)\\\\&=(1)\frac{1}{6}+(2)\frac{1}{6}+(3)\frac{1}{6}+(4)\frac{1}{6}+(5)\frac{1}{6}+(6)\frac{1}{6}\\\\&=\frac{1+2+3+4+5+6}{6}\\\\&=\frac{21}{6}\\\\&=\frac{7}{2}\\\\&=3.5\end{align}\end{split}\]

To summarize, we have the following:

\[E(X)=3.5\]

and thus:

\[\mu_X=3.5\]

Variance and Standard Deviation

Given the formula for variance, \(V(x) = E(X^2) - E(X)^2\), we first must calculate \(E(X^2)\) which is similar to the expected value calcuations above with the outcome values squared:

\[\begin{split}\begin{align}E(X^2) &= (1)^2\frac{1}{6}+(2)^2\frac{1}{6}+(3)^2\frac{1}{6}+(4)^2\frac{1}{6}+(5)^2\frac{1}{6}+(6)^2\frac{1}{6}\\\\&= (1)\frac{1}{6}+(4)\frac{1}{6}+(9)\frac{1}{6}+(16)\frac{1}{6}+(25)\frac{1}{6}+(36)\frac{1}{6}\\\\&= \frac{91}{6}\\\\&\approx 15.1667\end{align}\end{split}\]

Then, we find that:

\[\begin{split}\begin{align}V(X) &= E(X^2) - \mu_X^2\\\\&= \frac{91}{6} - \left(\frac{7}{2}\right)^2\\\\&= \frac{91}{6} - \frac{49}{4}\\\\&= \frac{182-147}{12}\\\\&= \frac{35}{12} \approx 2.91667\end{align}\end{split}\]

Finally, we can calculate the standard deviation as follows:

\[\begin{split}\begin{align}\sigma_X^2&= V(X)=\frac{35}{12}\implies \\\\ \sigma_X &=\sqrt{\frac{35}{12}}\\\\&\approx 1.70783 \end{align}\end{split}\]

Solution

Thus, the requested values are given below:

• \(E(X) = 3.5\)

• \(V(X) = \frac{35}{12}\)

• \(\sigma_X \approx 1.70783\)

Example: Spinner

Let’s agree that the spinner cannot land on the line between sectors. It can only land in a sector.

The spinner below has a 25% chance of landing on each sector. When it lands in a sector, the person spinning earns the number of points shown for that sector. Find the expected value, variance and standard deviation for a spin.

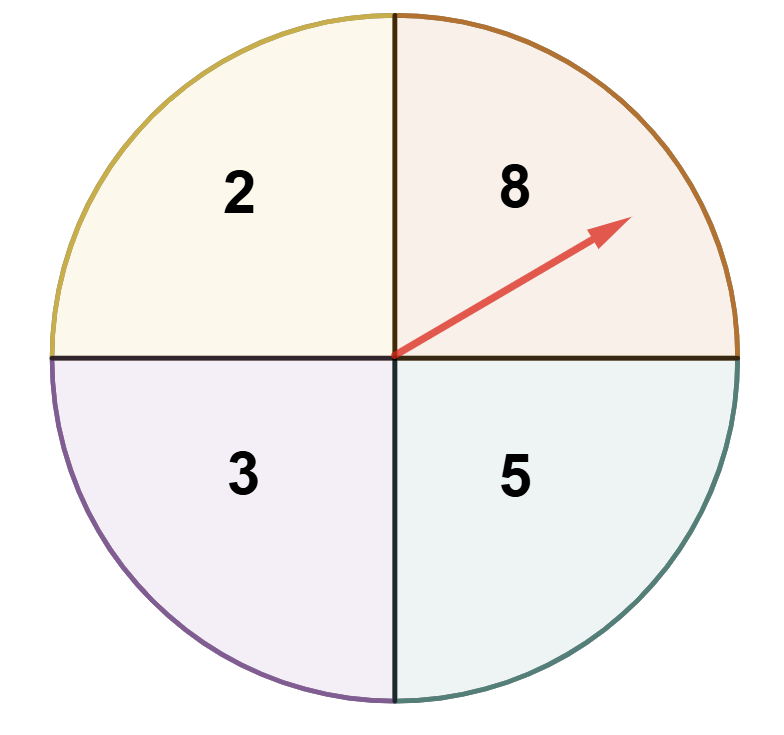
Expected Value

Let’s substitute and simplify efficiently:

\[\begin{split}\begin{align}E(X) &= \frac{2+3+5+8}{4} = \frac{18}{4}= \frac{9}{2}\\\\&=4.5\end{align}\end{split}\]

Variance and Standard Deviation

\[\begin{split}\begin{align}V(X) &= E(X^2) - \mu_X^2 \\\\ &= \frac{4+9+25+64}{5}-\left(\frac{9}{2}\right)^2\\\\&=\frac{102}{5}-\frac{81}{4}\\\\&=\frac{408-405}{10} = \frac{3}{20}\\\\&=0.15\end{align}\end{split}\]

Taking the square root, we find \(\sigma_X\) as follows:

\[\sigma_X = \sqrt{0.15} \approx 0.387298\]