Solutions to Exercises#
What is the probability that Shero flops exactly 2 pair given that she holds AJ?
Solution. Hint: restrict the probability space by removing an A and J from the deck. Instead of using the conditional probability formula, sometimes it is easier to simply work a standard probability question with a different probability space. We have 50 cards remaining in the deck, and two of the subsets in our value partition have only three cards, not four, since one Ace and one Jack are no longer in the deck. Let \(T\) be the event set of having exactly two pair after the flop.
An urn contains 7 red and 3 green marbles. The contents are thoroughly mixed, and two marbles are drawn (w/o replacement) one after the other. Find the probability that (a) red is drawn 2nd given that red was drawn first, (b) red is drawn 2nd given that green was drawn first, and (c) green is drawn 2nd given that green was drawn first.
Solution. The second draw occurs with one less marble, so we can update the probability space.
(a) With a red already drawn, the 2nd draw occurs with 6 red and 3 green: \(P(R|R) = \frac{6}{9} = \frac{2}{3}\).
(b) With a green already drawn, the 2nd draw occurs with 7 red and 2 green: \(P(R|G) = \frac{7}{9}\)
(c) With a green already drawn, the 2nd draw occurs with 7 red and 2 green: \( P(G|G) = \frac{2}{9}\)
You roll the dice in Monopoly on a turn where landing on Park Place or Boardwalk will bust you. You are 5 spaces from Park Place (7 from Boardwalk). You roll the dice, and one falls off the table and must be re-rolled. The other is 3. What is the probability you’ll go bust?
Solution. Before using our conditional probability formula, lets use our Monopoly Dice Roll chart: $\(P(\text{Busto} | 3) = \frac{P(\text{Busto} \cap 3)}{P(3)}=\frac{\frac{1}{3}}{\frac{1}{6}}\)\( \)\(P(\text{Busto} | 3) = \frac{2}{6}=\frac{1}{3}\)$
Then we see that:
Urn 1 has 3 red marbles and 2 blue. Urn 2 has 2 red marbles and 1 green. A marble is drawn at random from one of the urns. It is red. What is the probability it was drawn from Urn 2 if every marble, regardless of which urn it’s in, has an equal chance of being drawn?
Solution. The formula for conditional probability will be useful, so let’s identify some events. We’ll specify which urn the marble came from using \(U1\) and \(U2\), and then \(R\) for the event that a red marble was drawn.
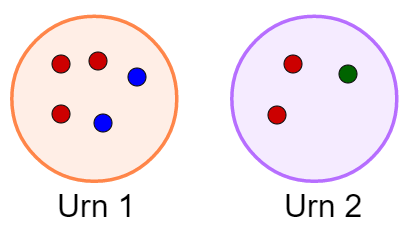
Fig. 10 width: 3cm#
We are asked about \(P(U2 | R)\), so we need to calculate \(P(U2 \cap R)\) and \(P(R)\). Noting that all marbles are equally likely to be chosen and glancing at the figure, we see that \(P(R)=\frac{5}{8}\) and \(P(R\cap U2)=\frac{2}{8}=\frac{1}{4}\). Then
Alternatively, we can consider the red marbles by themselves (restrict the probability space). If we draw one red marble from the five, what is the probability it’s in Urn 2? Well, 2 of the 5 are in Urn 2.
A math teacher gave her class two tests. If 25% of the class made A’s on both tests and 42% of the class made A’s on the first test, find the probability that someone who earned an A on Test 1 also earned an Aon Test 2. Soltuion. A quick Venn diagram is probably the best way to proceed, but the formula works, too.
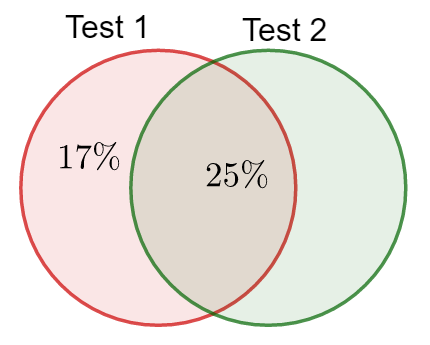
Fig. 11 width: 3cm#
Let events \(T1\) and \(T2\) indicate the A’s on Tests 1 and 2 respectively.
A jar contains black and white marbles. Two marbles are chosen without replacement. The probability of selecting a white marble second given that a black marble was drawn first is \(\frac{4}{5}\), and the probability of selecting a black marble on the first draw is \(\frac{1}{3}\). How many of each color marble is in the jar?
Solution. The probability of drawing a white marble changes.
On the first draw: \(P(W)= 1-P(B)=\frac{2}{3}\)
On the second draw, when a black marble has been removed on the first draw: \(P(W|B)=\frac{4}{5}\)
Because the probability has increased from
\[\frac{4}{6}\rightarrow\frac{4}{5},\]we deduce that there were six marbles originally, two black and four white.
In the United States, 56% of all children get an allowance and 41% of all children get an allowance and do household chores. What is the probability that a child does household chores given that the child gets an allowance?
Solution. Restricted probability space:
\[P=\frac{0.41}{0.56}\approx 0.73214\]
The Monte Hall problem is a classic conditional probability question that every math major should know about. An excellent discussion is posted at Brilliant.org.
The correct answer to the Monte Hall problem is to always switch doors, though this may trouble some very fine analytical minds. You should take the time to understand this problem and its solution.
Solution. We are calculating the following conditional probabilities given that we use the strategy of always switch:
The probability of winning given a car is picked first (and we thus switch to a goat): $\(P(W | \text{Car}) = 0\)$
The probability of winning given a goat is picked first (and we thus switch to a car): $\(P(W | \text{Goat}) = 1\)$
Since we have a \(\frac{1}{3}\) chance of picking a car first and a \(\frac{2}{3}\) chance of picking a goat first, we have the following probability:
This value is clearly higher than chance of a picking a car first and not switching, as you can verify.

