Compound Events#
Many interesting probability questions involve more than one thing happening. Here are two important examples:
What is the probability that, if we play one round of roullette, the outcome is either red or an even number?
What is the probability that a poker pro draws an Ace-King starting hand on both the next hand she plays and the one following that?
One simplistic mantra often heard in high school classrooms is that “OR means ADD and AND means MULTIPLY.” Not so fast. We have some conditions that must be satisfied. Here are more precise statements using set theory:
For disjoint event sets \(A\) and \(B\):
For independent event sets \(A\) and \(B\):
For the second statement, we also often use it for indpendent trials or Bournouli Trials. We’ll discuss details in a moment. Right now, the key idea is that if we have more than one event, we need to know how those events are related to be able to calculate the probability.
Example 2
Suppose we draw a single card at random from a well-shuffled standard deck of 52 cards. What is the probability of drawing a \(\spadesuit\) or a Queen?
Solution. The probability of drawing a spade is
and the probability of drawing a Queen is
But we can’t simply add the two outcomes:
For event sets, “either \(A\) or \(B\)” usually translates to \(A\cup B\), while “both \(A\) and \(B\)” indicates \(A\cap B\). High school students are sometimes taught: “If you see OR, add. But if you see AND, multiply.” Sadly, this is too simplistic and often incorrect. It’s much better to think in terms of sets. Note that:
\(n(Q)=4\)
\(n(S)=13\)
\(n(Q\cap S)=1\)
We have two different rules for calculating \(P(\text{A or B})\) depending whether the sets are disjoint:
For disjoint event sets: $\( P(A\cup B)=P(A)+P(B) \)$
Otherwise: $\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)$
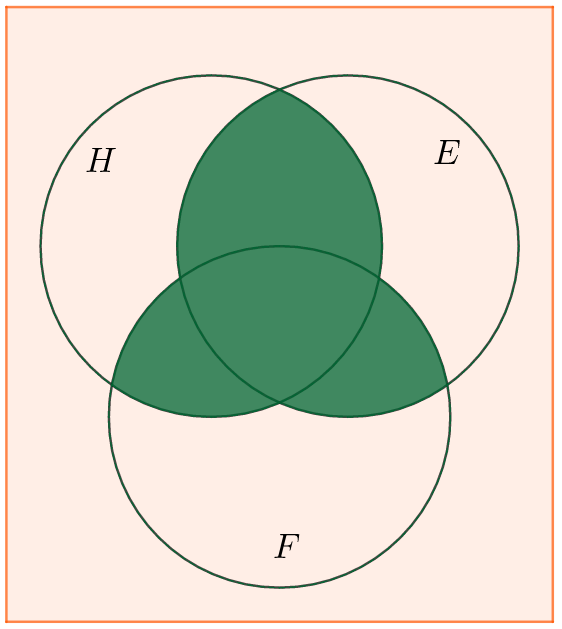
Sets \(A\) and \(B\) are disjoint provided \(A\cap B=\emptyset\). Note that when \(A\cap B=\emptyset \), then by definition \(P(A\cap B)=0\).
Consider the probability of drawing one card and getting both an Ace and an 8. The event sets are disjoint because they can never occur simultaneously. For non-disjoint sets, we must find a way to count \(|A\cap B|\).
When we have more than two sets, we use an idea called the principal of inclusion-exclusion. Use the Venn Diagram above to find all three 2-way intersections. They each get double-counted, so we need to the throw way the extra. As we do, we also end up throwing away the 3-way intersection – three times! We added the 3-way intersection three times, then subtracted it three times, so the final step is to add it back in exactly once. This is shown in the updated figure below.
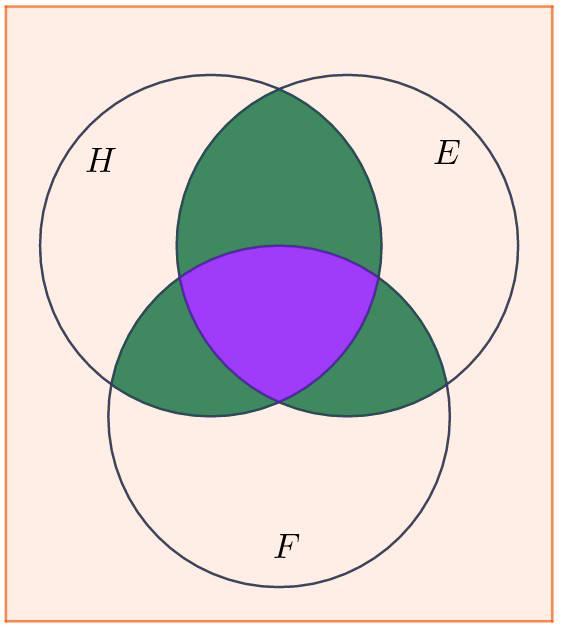
For three non-disjoint sets \(A\), \(B\) and \(C\), it looks like this:
The same idea works regardless of how many sets are involved, but the calculations are a bit tedious. In the grand old tradition of math texts, anything tedious is, of course, left to the reader.

